Resumen del post (5 minutos de lectura)
-
El problema de las 8 damas es un juego de ingenio que se desarrolla sobre el tablero de ajedrez
-
La consigna del juego es colocar 8 damas sobre el tablero de manera tal que ninguna de las 8 se ataque entre sí
-
Existen 92 distribuciones diferentes que cumplen con esta consigna, pero encontrar al menos 1 sin herramientas computacionales es una tarea tediosa y complicada
-
En este posteo se describen 3 métodos computacionales para resolver este problema
-
Para el desarrollo se utilizó lenguaje R sobre plataforma RStudio
-
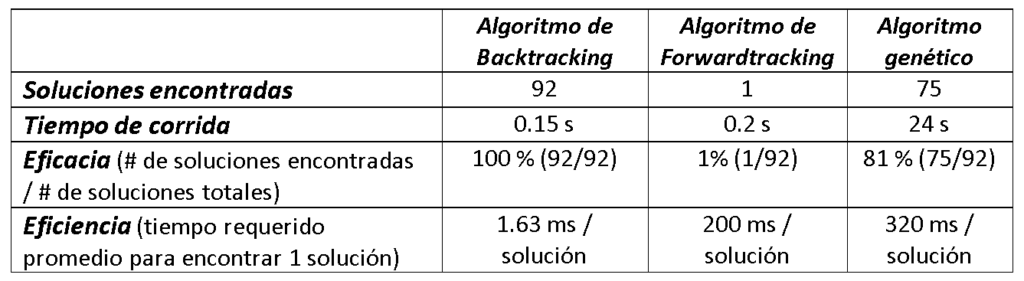
Los resultados de cada metodología se resumen en la siguiente tabla:
-
La metodología superior en todo sentido es el backtracking, tanto en eficacia (todas las soluciones encontradas) como en eficiencia (la más rápida en encontrar soluciones)
-
Por otro lado, el algoritmo genético es el método menos eficiente, requeriendo en promedio 320 ms para encontrar una solución
-
Finalmente, el algoritmo de forwardtracking es el menos eficaz en términos de encontrar soluciones (1 solución con el patrón especificado de búsqueda)
Post completo (15 minutos)
Aunque el problema de las 8 damas sobre el tablero de ajedrez es bien conocido, el siguiente video de YouTube lo describe con gran detalle:
Si bien es posible resolverlo de forma manual (si tienen mucho tiempo de sobra y quieren intentarlo, son bienvenidos!), la manera más tradicional de resolverlo computacionalmente es a través de algoritmos de backtracking, tal como se describe acá:
Son varios los videos que muestran cómo resolver este problema a través de algoritmos generados en Java, Python o C++, pero no encontré ninguno que lo haya implementado en R. Por lo tanto, en este artículo se describe la implementación de 3 metodologías diferentes de resolución (total o parcial) del problema de las 8 reinas en R. Los 3 métodos son:
- Algoritmo de Backtracking
- Algoritmo “forwardtracking” (o el “método del cavernícola”!)
- Algoritmo genético
Algoritmo de backtracking
El algoritmo desarrollado se basa en el concepto de este video, en donde cada celda de la matríz de 1×8 representan las columnas del tablero y el valor en cada celda representa la fila en la que se sitúa la dama de esa columna
Para el código de R se utiliza solo R base, aunque es necesario instalar el paquete “rchess” para poder graficar las soluciones encontradas.
PASO 1: definir el número de damas a utilizar
nQueens<-8 PASO 2: definir matrices de trabajo y de almacenamiento de soluciones:
Solutions <- matrix(data = list(),nrow=1,ncol=0)
arrayQueens<-matrix(0,ncol=nQueens)
ActiveCol = 1
ActiveValue =1
counterSol=1 La matríz “arrayQueens” es la matríz de 1×8 en donde se generan las disposiciones de las damas (técnicamente es una matríz de 1xN columnas, para poder escalar el problema a N Damas sobre un tablero de dimensiones NxN)
PASO 3: definir el loop por el cual se va a iterar para encontrar las soluciones
repeat{ Nótese que el comando “repeat” entra en un loop sin fin, por lo que es necesario especificar dentro del código el punto de salida del mismo para que finalice el proceso
PASO 4: inicializar variables, asignar valores y evaluar ataques entre damas
nro_attacks <- 0
arrayQueens[ActiveCol]=ActiveValue
for (evalAttackBtQueens in 1:(ActiveCol-1)){
if (ActiveCol ==1){
ActiveCol == ActiveCol + 1
break
}
if (arrayQueens[evalAttackBtQueens]== arrayQueens[ActiveCol]||
abs(arrayQueens[evalAttackBtQueens]-arrayQueens[ActiveCol])==abs(evalAttackBtQueens-ActiveCol)){
nro_attacks = nro_attacks +1
}
next
} El “if” final evalúa si la nueva dama comparte la misma fila con alguna dama que haya sido colocada previamente o se encuentra en la misma diagonal (no se evalúa interacción entre columnas dado que cada dama, por default, se sitúa en una columna diferente representada por las celdas de la matríz “arraQueens”
PASO 5: Evaluar interacciones entre damas, guardar soluciones, moverse entre columnas
if (nro_attacks>0 && ActiveValue < nQueens){
ActiveValue = ActiveValue +1
}else if (nro_attacks>0 && ActiveValue == nQueens){
if (arrayQueens[ActiveCol-1]==nQueens && ActiveCol == 2){
break
}else if (arrayQueens[ActiveCol-1]==nQueens && ActiveCol > 2){
ActiveValue = arrayQueens[ActiveCol-2] + 1
ActiveCol = ActiveCol -2
}else{
ActiveValue = arrayQueens[ActiveCol-1] + 1
ActiveCol = ActiveCol -1
}
}else if (nro_attacks==0){
if (ActiveCol==nQueens){
Solutions[[counterSol]] <- arrayQueens
counterSol = counterSol + 1
if(ActiveValue==nQueens){
ActiveValue = arrayQueens[ActiveCol-1]+1
ActiveCol = ActiveCol -1
#print(ActiveCol)
}else{
ActiveValue = ActiveValue +1
}
}else{
ActiveValue = 1
ActiveCol = ActiveCol +1
}
} El código evalúa si hay interacciones entre damas (variable “nro_attacks” > 0) o si no las hay luego de agregar una nueva dama al proceso. En caso de haberla, el código retrocede 1 columna y comienza a colocar damas nuevamente (lo que conforma la esencia del backtracking). En caso de no encontrar interacciones, avanza a la siguiente columna continúa colocando damas.
SI no hay interacciones y se han logrado colocar N damas en el tablero entonces esa configuración de damas en el tablero es una solución. Todas las soluciones se guardan como listas en la matríz “Solutions”.
La salida del loop “Repeat” se da cuando el proceso ha cubierto todo el tablero a través del procedimiento de backtraking.
El tiempo de ejecución del proceso para 8 damas es de 0.136 segundos, o 1/10 de segundo. Se encontraron las 92 soluciones que existen para 8 damas.
Abajo se muestran algunas de las soluciones, graficadas en RStudio con el paquete “rchess”

Algoritmo de “forwardtrackig” (o método del cavernícola)
Este es el primer algoritmo con el qué encontré soluciones al problema de las 8 damas (la implementación fue hace unos cuantos años y en Visual Basic). Es eficiente en términos de resolución del problema pero no es nada eficaz y difícilmente pueda encontrar las 92 soluciones posibles (siempre considerando 8 damas en el tablero. El número de soluciones varia si se consideran tableros con más o menos casilleros).
El algoritmo trabaja de la siguiente manera: coloca damas en el tablero comenzando por la esquina superior izquierda, recorriendo las filas y
encontrando casilleros no atacados para ubicar las siguientes. Si una disposición no es exitosa (no se logra ubicar las 8 damas) se mueve la primer dama 1 casillero hacia la derecha y se vuelve a aplicar el mismo criterio de búsqueda.
El problema con esta metodología es que el espectro de soluciones está acotado al patrón de búsqueda inicial. Dicho de otra manera, el
algoritmo no evalúa todas las soluciones posibles (tal como ocurre en el algoritmo de backtracking), solo aquellas que concuerdan con el patrón de avance especificado El código en R está basado en el desarrollo original en Visual Basic, lo que implique que obviamente se puede optimizar:
PASO 1: Definir influencia de 1° dama
for (i in 1:8){
for (ii in 1:8){
runCounter = runCounter +1
#print(runCounter)
board[]=0
# print(board)
Queen = 1
#Queen 1 influence
board[1:8,ii]=11*Queen
board[i,1:8]=11*Queen
qrow=i
qcol=ii
while(qrow >0 && qrow <9 && qcol >0 && qcol <9 ){
board[qrow,qcol] <- 11*Queen
qrow = qrow+1
qcol = qcol+1
}
qrow = i
qcol = ii
while(qrow >0 && qrow <9 && qcol >0 && qcol <9 ){
board[qrow,qcol] =11*Queen
qrow = qrow-1
qcol = qcol+1
}
qrow = i
qcol = ii
while(qrow >0 && qrow <9 && qcol >0 && qcol <9 ){
board[qrow,qcol] =11*Queen
qrow = qrow+1
qcol = qcol-1
}
qrow = i
qcol = ii
while(qrow >0 && qrow <9 && qcol >0 && qcol <9 ){
board[qrow,qcol] =11*Queen
qrow = qrow-1
qcol = qcol-1
}
board[i,ii]=Queen
aux_board[i,ii]=Queen
Queen = Queen + 1
PASO 2: Definir influencia de 2° y demás damas
#Queens 2 to 8 influence
for (q in 2:8){
if (Queen == 9){
break
}
for (row_id in 1:8){
if (Queen == 9){
break
}
if (is.even(Queen)==TRUE && revertSearchingPath == 1){
row = 9-row_id
}else{
row=row_id
}
for (col_id in 1:8){
if (Queen == 9){
break
}
if (is.even(Queen)==TRUE && revertSearchingPath == 1){
col = 9-col_id
row = 9-row_id
}else{
row=row_id
col=col_id
}
if (board[row,col]==0){
board[1:8,col]=11*Queen
board[row,1:8]=11*Queen
qrow <- row
qcol <- col
#print(qcol)
while(qrow >0 && qrow <9 && qcol >0 && qcol <9 ){
board[qrow,qcol] <- 11*Queen
qrow = qrow+1
qcol = qcol+1
}
qrow = row
qcol = col
while(qrow >0 && qrow <9 && qcol >0 && qcol <9 ){
board[qrow,qcol] =11*Queen
qrow = qrow-1
qcol = qcol+1
}
qrow = row
qcol = col
while(qrow >0 && qrow <9 && qcol >0 && qcol <9 ){
board[qrow,qcol] =11*Queen
qrow = qrow+1
qcol = qcol-1
}
qrow = row
qcol = col
while(qrow >0 && qrow <9 && qcol >0 && qcol <9 ){
board[qrow,qcol] =11*Queen
qrow = qrow-1
qcol = qcol-1
}
board[row,col]=Queen
aux_board[row,col]=Queen
PASO 3: Guardar soluciones en caso de lograr colocar 8 damas en el tablero
En caso de que no se haya llegado a las 8 damas en el tablero, se adiciona una dama más y se vuelve a correr el procedimiento de búsqueda.
if (Queen == 8){
print("8 queens!")
board <- replace(board, board[,] > 10, NA)
solutions[[counterSol]] <- t(which(board <10,arr.ind = TRUE))[1,]
counterSol = counterSol +1
print(board)
# Sys.sleep(1)
}
Queen = Queen +1
# print ("aca")
}
}
}
}
}
}
Con esta configuración, el algoritmo encuentra 1 sola distribución de 8 damas que no se atacan entre sí contra las 92 soluciones que encuentra el algoritmo de backtracking (en realidad se encuentran 4 soluciones, porque la distribución encontrada se puede rotar ¼ de vuelta sobre el tablero para generar otras 3 soluciones adicionales a la informada).
La siguiente matríz de 8×8 permite visualizar la ubicación de las damas sobre el tablero. Los nros indican la secuencia en la que se fueron disponiendo las damas en el mismo (por ej: el “1” indica que esa fue la primer dama que se colocó, “2” la segunda y así sucesivamente).
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
[1,] NA 2 NA NA NA NA NA NA
[2,] NA NA NA 3 NA NA NA NA
[3,] NA NA NA NA NA 4 NA NA
[4,] NA NA NA NA NA NA NA 5
[5,] NA NA 6 NA NA NA NA NA
[6,] 1 NA NA NA NA NA NA NA
[7,] NA NA NA NA NA NA 7 NA
[8,] NA NA NA NA 8 NA NA NA
La corrida tomó 0,2 segundos, lo que demuestra que no es un método eficiente de búsqueda de soluciones.
Algoritmo genético
De la misma manera que el método anterior, los algoritmos genéticos no resultan un método eficiente en encontrar todas las soluciones del problema. Sin embargo, es mucho más eficiente que el algoritmo de forwardtracking en términos de cantidad de soluciones encontradas.
Para esta metodología se requiere instalar el paquete “GA” en RStudio.
PASO 1: Definir la función costo (o función objetivo)
Es la función que el GA debe minimizar para encontrar soluciones. Mide la cantidad de interacciones entre damas para cada solución generada por el GA:
#Libraries and functions
library ("rchess")
library ("GA")
fitnessFun <- function(individual){
nro_attacks = 0
for (Queen in 1:length(individual)){ #for each Queen...
for (evalAttackBtQueens in 1:length(individual)){ #... and for each column
if (Queen != evalAttackBtQueens){
if (individual[evalAttackBtQueens]== individual[Queen]||
abs(individual[evalAttackBtQueens]-individual[Queen])==abs(evalAttackBtQueens-Queen)){
nro_attacks = nro_attacks +1
}
}
next
}
next
}
return(nro_attacks)
} PASO 2: Definir el número de damas a utilizar y la solución de arranque del GA
La función de GA requiere que se le especifique una solución de arranque (la función la denomina “sugerencia”) para asumirla como la solución “padre” a partir de la cual va a generar múltiples soluciones “hijo” en base a los parámetros de crossover y mutación especificados por el usuario. Para este caso se le indica una solución aleatoria cualquiera:
nQueens<- 8
ind2 <- c(5,2,8,1,5,3,4,6) PASO 3: Generar el GA
GA <- ga(type = "permutation",
fitness = function(x) -fitnessFun(c(x[1], x[2],x[3], x[4],x[5], x[6],x[7], x[8])),
lower = c(1,1,1,1,1,1,1,1), upper = c(8,8,8,8,8,8,8,8), suggestions = ind2,
popSize = 100, maxiter = 800, run = 300) No se modificaron los parámetros de crossover (pcrossover) o mutación (pmutation). Solamente se realizó una sensibilidad al número de children por generación (popSize), número de generaciones a correr (maxiter) y el número máximo de generaciones sin mejora en la función costo (run).
Con los valores indicados (popSize = 100, maxiter = 800, run = 300) el algoritmo genera 300 generaciones de 100 individuos en 0,5 s antes de detenerse por alcanzar el número máximo de generaciones con el mismo error.
Desde el punto de vista de la eficacia, el summary el proceso indica que se encontraron solo 6 de las 92 soluciones posibles:
> summary(GA)
-- Genetic Algorithm -------------------
GA settings:
Type = permutation
Population size = 100
Number of generations = 800
Elitism = 5
Crossover probability = 0.8
Mutation probability = 0.1
Suggestions =
x1 x2 x3 x4 x5 x6 x7 x8
1 5 2 8 1 3 3 4 3
GA results:
Iterations = 300
Fitness function value = 0
Solutions =
x1 x2 x3 x4 x5 x6 x7 x8
[1,] 5 7 2 6 3 1 8 4
[2,] 5 1 8 4 2 7 3 6
[3,] 7 3 8 2 5 1 6 4
[4,] 3 6 2 7 5 1 8 4
[5,] 5 7 2 4 8 1 3 6
[6,] 7 2 4 1 8 5 3 6 Esto evidencia que, de las 300 generaciones que se corrieron, la mayoría de los individuos (children) con mejor función costo (fitness = 0, o sea, sin interacciones entre las 8 damas) eran idénticos entre sí.
Para incrementar el número de soluciones encontradas, se puede:
- Incrementar la P crossover / P mutación para generar más variabilidad y diversidad
- Incrementar el número de individuos por generación para generar mayor variabilidad
Se elige la alternativa (2) y se aumenta en número de individuos por generación a 1500. Los resultados son:
Tiempo de corrida: 25.6 s (significativamente mayor que la configuración anterior)
> summary(GA)
-- Genetic Algorithm -------------------
GA settings:
Type = permutation
Population size = 1500
Number of generations = 800
Elitism = 75
Crossover probability = 0.8
Mutation probability = 0.1
Suggestions =
x1 x2 x3 x4 x5 x6 x7 x8
1 5 2 8 1 5 3 4 6
GA results:
Iterations = 300
Fitness function value = 0
Solutions =
x1 x2 x3 x4 x5 x6 x7 x8
[1,] 6 4 1 5 8 2 7 3
[2,] 2 7 5 8 1 4 6 3
[3,] 6 4 7 1 8 2 5 3
[4,] 2 6 1 7 4 8 3 5
[5,] 3 6 2 7 1 4 8 5
[6,] 8 4 1 3 6 2 7 5
[7,] 4 8 1 5 7 2 6 3
[8,] 7 2 4 1 8 5 3 6
[9,] 2 5 7 4 1 8 6 3
[10,] 5 7 2 6 3 1 8 4
...
[74,] 6 2 7 1 3 5 8 4
[75,] 4 8 1 3 6 2 7 5
En definitiva, el número de generaciones evaluadas no varia (300 generaciones), pero esta vez se encontraron 75 soluciones de las 92 existentes. El tiempo requerido fue de 24 s.
Conclusiones
Los resultados de cada metodología se resumen en la siguiente tabla:

La metodología superior en todo sentido es el backtracking, tanto en eficacia (todas las soluciones encontradas) como en eficiencia (la más rápida en encontrar soluciones)
Por otro lado, el algoritmo genético es el método menos eficiente, requeriendo en promedio 320 ms para encontrar una solución
Finalmente, el algoritmo de forwardtracking es el menos eficaz en términos de encontrar soluciones (1 solución con el patrón especificado de búsqueda)
